解密高階斜率:駕馭金融市場複雜性的利器
[免責聲明] 本文僅供教育和資訊目的,不構成投資建議。讀者在做出任何投資決定前應諮詢合格的金融專業人士。
在上一篇文章中,我們探討了斜率分析的基礎和簡單應用。今天,我們將深入高階斜率計算方法。這個在金融市場分析中日益重要的工具。它不僅能幫助我們應對市場的複雜性,也能為投資決策提供更精準的指引。
① 對數報酬率斜率及其優勢
在金融市場分析中,對數報酬率斜率是一個強大而又常被忽略的工具。與普通的價格斜率相比,對數收益率斜率有著顯著的優勢,特別是在處理長期趨勢和不同價格尺度的資產時。
首先,讓我們先理解什麼是對數收益率。對數收益率是指資產價格自然對數的變化。數學表達式為:
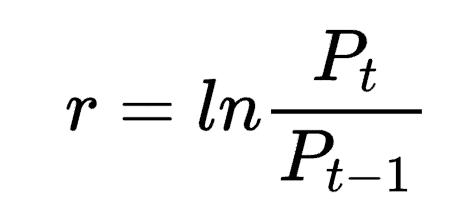
其中,r是對數收益率,Pt是當前價格,Pt-1是前一期價格。
對數報酬率斜率的計算方法是將一段時間的對數報酬率進行線性迴歸,得到的斜率就是我們所需的對數報酬率斜率。
對數收益率斜率的主要優點包括:
- 標準化:對數報酬率可以標準化不同價格水準的資產,使得高價格和低價格的資產可以直接比較。
- 複利效應:對數報酬率能更反映複利效應,這在長期分析中尤其重要。
- 對稱性:對數報酬率在正負方向上是對稱的,這使得上漲和下跌的幅度更容易比較。
- 穩定性:對數收益率通常比普通收益率更穩定,減少了極端值的影響。
讓我們透過一個簡單的Python範例來說明如何計算對數收益率斜率:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns
# 設定 seaborn 樣式
sns.set_style("whitegrid") # 或使用 "darkgrid", "white", "dark", "ticks"
# 建立畫布和子圖
fig, axes = plt.subplots(2, 1, figsize=(15, 12), sharex=True)
# 設定配色方案(可選)
sns.set_palette("husl")
# 原始價格圖
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices')
axes[0].legend()
axes[0].grid(True)
# 對數收益率斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['log_slope'], label=f'{asset} Log Slope')
axes[1].set_title('Log Return Slopes')
axes[1].legend()
axes[1].grid(True)
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 調整x軸標籤
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自動調整日期標籤的格式
# 調整子圖之間的間距
plt.tight_layout()
# 顯示圖形
plt.show()
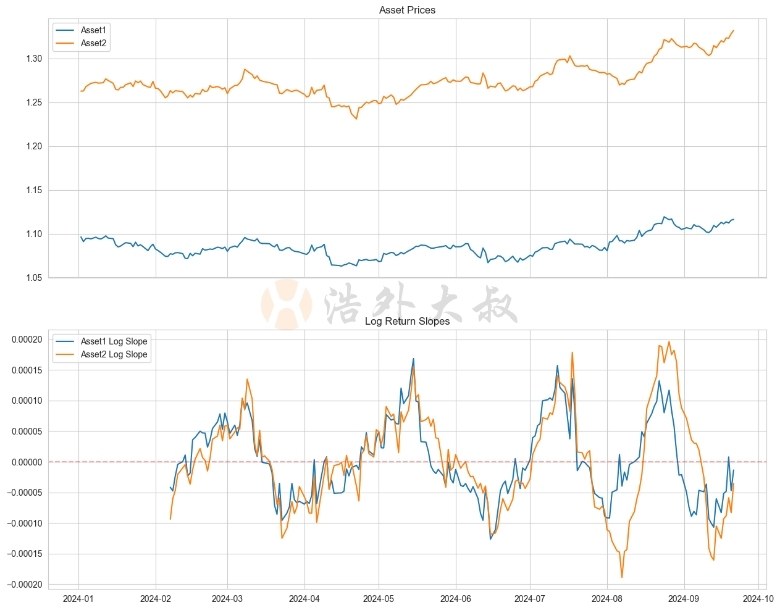
這個函數計算了一個滾動視窗內的對數收益率斜率。透過調整視窗大小,我們可以捕捉不同時間尺度的趨勢。
在實際應用中,對數報酬率斜率可以幫助我們識別長期趨勢,比較不同資產類別的表現,甚至在跨市場分析中發揮作用。例如,當我們比較一個高價股票和一個低價股票的趨勢時,對數報酬率斜率可以提供更公平的比較基礎。
然而,需要注意的是,對數收益率斜率雖然強大,但並非萬能。在短期分析或高頻交易中,普通價格斜率可能更直觀。因此,選擇合適的斜率計算方法應該根據具體的分析目的和時間範圍來決定。
雖然對數收益率斜率提供了許多優勢,但在多時間框架分析中如何有效應用此方法呢?我們將在未來的文章中深入探討這個問題,並展示如何將不同時間尺度的斜率分析整合起來,以獲得更全面的市場視角。
在下一節中,我們將探討如何處理非線性趨勢,這是金融市場中常見的複雜情況。透過多項式迴歸,我們可以捕捉更複雜的市場動態,為我們的分析工具箱增添新的利器。
② 非線性趨勢與多項式迴歸
金融市場中的趨勢往往不是簡單的直線,而是呈現各種複雜的非線性模式。這就是為什麼我們需要更高級的技術來捕捉這些複雜的市場動態。多項式迴歸就是這樣一個強大的工具,它可以幫助我們模擬和分析非線性趨勢。
多項式迴歸是線性迴歸的擴展,它使用多項式函數來模擬資料的曲線關係。一般形式為:
y = β₀ + β₁x + β₂x² + ... + βₙxⁿ + ε
其中,n是多項式的階數,β是係數,ε是誤差項。
在金融市場分析中,多項式迴歸可以幫助我們:
- 捕捉複雜的市場週期
- 辨識潛在的反轉點
- 更準確預測短期和中期趨勢
讓我們透過一個Python範例來說明如何使用多項式迴歸分析市場趨勢:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import seaborn as sns
def polynomial_regression_slope(prices, degree=2, window=30):
"""
使用多項式迴歸計算斜率
"""
# 預先建立儲存結果的Series,填滿NaN
slopes = pd.Series(np.nan, index=prices.index)
x = np.arange(window).reshape(-1, 1)
poly_features = PolynomialFeatures(degree=degree, include_bias=False)
x_poly = poly_features.fit_transform(x)
for i in range(window, len(prices)):
y = prices.iloc[i-window:i]
if not y.isna().any(): # 確保沒有缺失值
model = LinearRegression()
model.fit(x_poly, y)
# 計算最後一點的斜率
last_x = x_poly[-1].reshape(1, -1)
slope = np.sum(model.coef_ * last_x * np.arange(1, degree+1))
slopes.iloc[i] = slope
return slopes
# 計算斜率
window = 30
results = {}
for asset in ['Asset1', 'Asset2']:
results[asset] = {
'poly_slope': polynomial_regression_slope(df[asset], degree=3, window=window),
}
# 設定 seaborn 樣式
sns.set_style("whitegrid")
sns.set_palette("husl")
# 建立畫布和子圖
fig, axes = plt.subplots(2, 1, figsize=(15, 12), sharex=True)
# 原始價格圖
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices', fontsize=12, pad=10)
axes[0].legend()
# 多項式迴歸斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['poly_slope'], label=f'{asset} Poly Slope')
axes[1].set_title('Polynomial Regression Slopes (Degree 3)', fontsize=12, pad=10)
axes[1].legend()
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 新增零線參考
# 調整x軸標籤
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自動調整日期標籤的格式
# 調整子圖之間的間距
plt.tight_layout()
# 顯示圖形
plt.show()
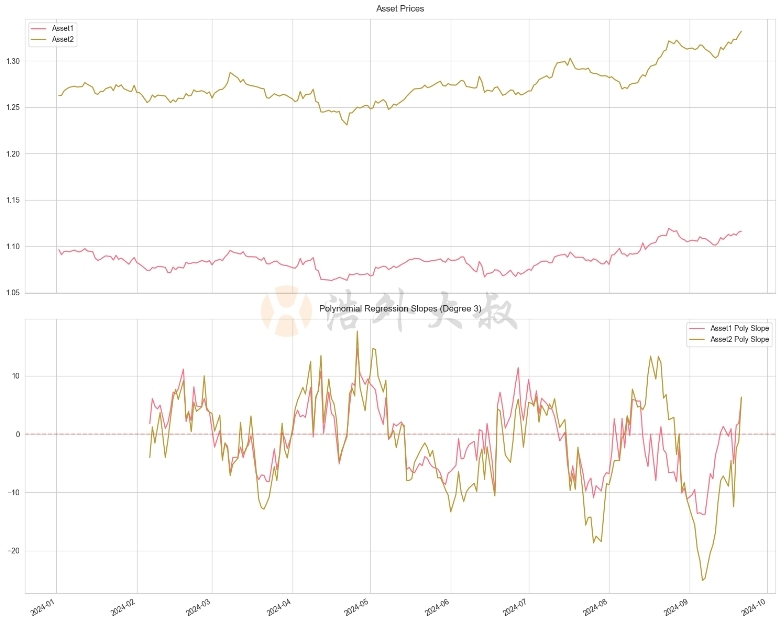
在這個例子中,我們使用了3階多項式迴歸來計算斜率。這種方法可以捕捉更複雜的價格模式,例如加速上漲或減速下跌的趨勢。
多項式迴歸的關鍵優勢是它可以適應各種市場條件。例如,在牛市初期,我們可能會看到一個上凸的曲線,而在市場頂部附近,曲線可能會變得平緩或開始下彎。透過觀察多項式迴歸的斜率變化,我們可以更早地辨識這些潛在的市場轉折點。
然而,使用多項式迴歸時也需要注意幾個問題:
- 過度擬合:高階多項式可能會過度擬合數據,導致對雜訊過於敏感。
- 參數選擇:選擇適當的多項式階數和視窗大小至關重要。
- 計算複雜度:高階多項式迴歸的計算量較大,可能不適合高頻交易。
在實際應用中,我通常會結合不同階數的多項式迴歸,以獲得更全面的市場視角。例如,2階多項式可以幫助識別整體趨勢,而3階或4階多項式則可以捕捉更細微的市場動態。
在下一節中,我們將探討如何使用動態時間視窗來進一步提高斜率計算的準確性和適應性。這種方法可以幫助我們更好地應對市場波動性的變化,為我們的分析提供更精確的工具。
③ 動態時間視窗在斜率計算的應用
在金融市場分析中,固定時間視窗的斜率計算方法雖然簡單直觀,但往往難以適應市場波動性的變化。這就是為什麼動態時間視窗在斜率計算中變得越來越重要。動態時間視窗可以根據市場條件自動調整,從而提供更準確和及時的趨勢訊號。
動態時間窗口的核心思想是根據市場的波動性來調整計算斜率所使用的時間窗口大小。在波動性較低的市場中,我們可以使用較大的時間窗口來減少噪音的影響;而在高波動性市場中,較小的時間窗口可以幫助我們更快地捕捉趨勢變化。
以下是一個使用動態時間視窗計算斜率的Python範例:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import seaborn as sns
def dynamic_window_slope(prices, min_window=10, max_window=50, volatility_lookback=20):
"""
使用動態時間視窗計算斜率
參數:
prices: 價格序列
min_window: 最小視窗大小
max_window: 最大視窗大小
volatility_lookback: 計算波動率的回看期
"""
# 預先建立儲存結果的Series,填滿NaN
slopes = pd.Series(np.nan, index=prices.index)
# 計算波動率
returns = prices.pct_change()
volatility = returns.rolling(window=volatility_lookback).std()
# 處理極端值和缺失值
volatility = volatility.fillna(0) # 填充NA值
# 如果所有值都相同,直接使用最大窗口
if volatility.min() == volatility.max():
dynamic_window = pd.Series(max_window, index=prices.index)
else:
# 計算動態視窗大小
normalized_vol = (volatility - volatility.min()) / (volatility.max() - volatility.min())
dynamic_window = ((1 - normalized_vol) * (max_window - min_window) + min_window)
# 確保窗口大小在合理範圍內
dynamic_window = dynamic_window.clip(min_window, max_window)
# 轉換為整數
dynamic_window = dynamic_window.astype(int)
# 計算斜率
for i in range(max_window, len(prices)):
window = dynamic_window.iloc[i]
x = np.arange(window)
y = prices.iloc[i-window:i]
if not y.isna().any(): # 確保沒有缺失值
try:
slope, _ = np.polyfit(x, y, 1)
slopes.iloc[i] = slope
except:
continue
return slopes
# 計算斜率
window = 30
results = {}
for asset in ['Asset1', 'Asset2']:
results[asset] = {
'dynamic_slope': dynamic_window_slope(df[asset])
}
# 設定 seaborn 樣式
sns.set_style("whitegrid")
sns.set_palette("husl")
# 建立畫布和子圖
fig, axes = plt.subplots(2, 1, figsize=(15, 12), sharex=True)
# 原始價格圖
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices', fontsize=12, pad=10)
axes[0].legend()
# 動態視窗斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['dynamic_slope'], label=f'{asset} Dynamic Slope')
axes[1].set_title('Dynamic Window Slopes', fontsize=12, pad=10)
axes[1].legend()
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 新增零線參考
# 調整x軸標籤
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自動調整日期標籤的格式
# 調整子圖之間的間距
plt.tight_layout()
# 顯示圖形
plt.show()
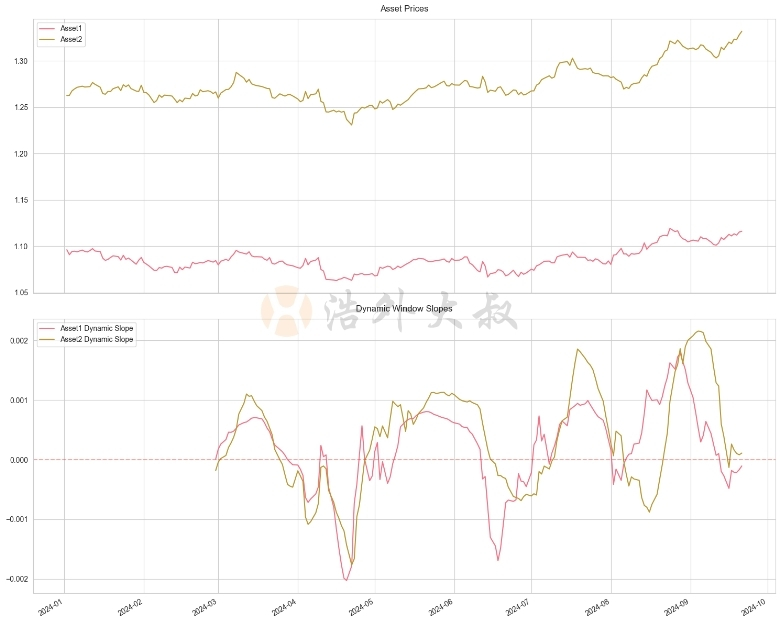
在這個例子中,我們根據市場的波動性動態調整時間視窗的大小。當波動性增加時,視窗變小,使得斜率計算更快響應市場變化;當波動性減少時,視窗變大,提供更平滑的趨勢訊號。
動態時間視窗方法的主要優點包括:
- 適應性強:能夠自動適應不同的市場條件。
- 訊號品質提升:在不同波動環境下提供更準確的趨勢訊號。
- 降低滯後性:在高波動期能更快捕捉趨勢變化。
然而,使用動態時間視窗時也需要注意以下幾點:
- 參數選擇:最小和最大視窗大小以及波動性計算的回溯期需要謹慎選擇。
- 計算複雜度:相較於固定窗口,動態窗口方法的計算量較大。
- 過度敏感:在某些情況下可能會對短期波動過度敏感。
在實際應用中,我經常將動態時間視窗方法與其他技術指標結合使用。例如,可以將動態視窗斜率與相對強弱指數(RSI)或移動平均線結合,以獲得更全面的市場視角。
這種方法特別適合那些波動性經常變化的市場,如外匯市場或某些高波動性的股票。透過動態調整分析的時間框架,我們可以更好地掌握市場的脈搏,並做出更明智的投資決策。
多項式迴歸為我們提供了處理非線性趨勢的強大工具。然而,如何選擇最佳的多項式階數呢?在後續文章中,我們將探討如何使用機器學習技術來自動最佳化這些參數,進一步提高我們的分析精確度。
在下一節中,我們將透過一個具體的案例研究,比較不同斜率計算方法在股票趨勢分析中的表現。這將幫助我們更好地理解這些方法的實際應用價值,並為選擇適當的分析工具提供指導。
④ 個案研究:比較不同斜率計算法在股票趨勢分析上的表現
為了更好地理解不同斜率計算方法的實際應用價值,讓我們透過一個具體的案例來比較它們在股票趨勢分析中的表現。我們將使用歷史資料作為例子,比較簡單線性迴歸、對數報酬率斜率、多項式迴歸斜率和動態時間視窗斜率這四種方法。
首先,讓我們取得數據並實作這些方法:
def simple_slope(prices, window=30):
"""
使用簡單線性迴歸計算斜率
參數:
prices: pandas Series, 價格序列
window: int, 計算斜率的視窗大小
返回:
pandas Series, 包含斜率值,索引與輸入資料對應
"""
# 預先建立儲存結果的Series,填滿NaN
slopes = pd.Series(np.nan, index=prices.index)
# 準備用於回歸的X值(時間索引)
x = np.arange(window)
# 計算斜率
for i in range(window, len(prices) + 1):
# 取得視窗內的價格數據
y = prices.iloc[i-window:i]
# 檢查是否有缺失值
if not y.isna().any():
try:
# 使用 scipy.stats 的 linregress 計算斜率
slope, _, _, _, _ = stats.linregress(x, y)
slopes.iloc[i-1] = slope
except:
continue
return slopes
# 為兩個資產計算不同類型的斜率
window = 30
results = {}
for asset in ['Asset1', 'Asset2']:
results[asset] = {
'simple_slope': simple_slope(df[asset], window),
'log_slope': log_return_slope(df[asset], window),
'poly_slope': polynomial_regression_slope(df[asset], degree=3, window=window),
'dynamic_slope': dynamic_window_slope(df[asset])
}
# 設定 seaborn 樣式
sns.set_style("whitegrid")
sns.set_palette("husl")
# 建立畫布和子圖
fig, axes = plt.subplots(5, 1, figsize=(15, 12), sharex=True)
# 原始價格圖
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices', fontsize=12, pad=10)
axes[0].legend()
# 簡單斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['simple_slope'], label=f'{asset} Simple Slope')
axes[1].set_title('Simple Slopes', fontsize=12, pad=10)
axes[1].legend()
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 新增零線參考
# 對數收益率斜率
for asset in ['Asset1', 'Asset2']:
axes[2].plot(df.index, results[asset]['log_slope'], label=f'{asset} Log Slope')
axes[2].set_title('Log Return Slopes', fontsize=12, pad=10)
axes[2].legend()
axes[2].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 新增零線參考
# 多項式迴歸斜率
for asset in ['Asset1', 'Asset2']:
axes[3].plot(df.index, results[asset]['poly_slope'], label=f'{asset} Poly Slope')
axes[3].set_title('Polynomial Regression Slopes (Degree 3)', fontsize=12, pad=10)
axes[3].legend()
axes[3].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 新增零線參考
# 動態視窗斜率
for asset in ['Asset1', 'Asset2']:
axes[4].plot(df.index, results[asset]['dynamic_slope'], label=f'{asset} Dynamic Slope')
axes[4].set_title('Dynamic Window Slopes', fontsize=12, pad=10)
axes[4].legend()
axes[4].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 新增零線參考
# 調整x軸標籤
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自動調整日期標籤的格式
# 新增總標題
fig.suptitle('Comparison of Different Slope Calculation Methods',
fontsize=14, y=1.02)
# 調整子圖之間的間距
plt.tight_layout()
# 顯示圖形
plt.show()
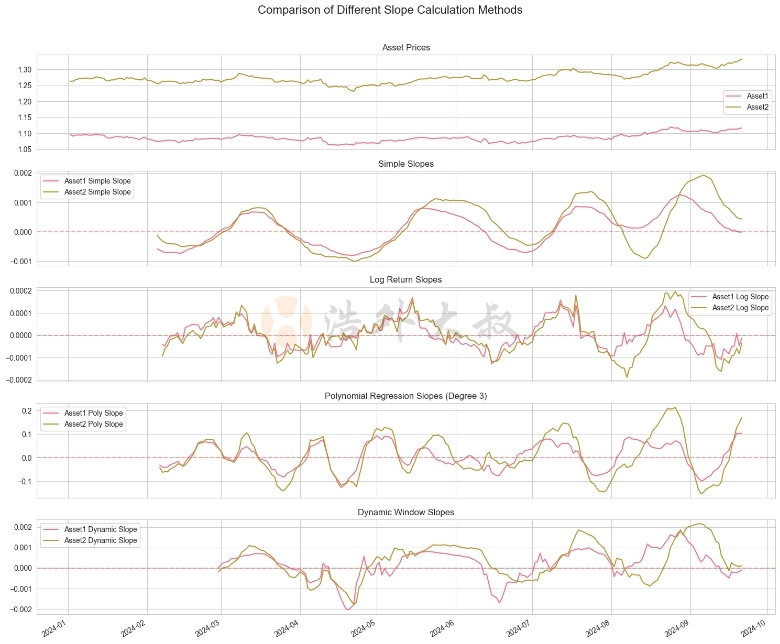
這段程式碼實現了四種不同的斜率計算方法,並將它們應用於蘋果公司的股票數據。讓我們來分析一下每種方法的表現:
- 簡單線性迴歸斜率:此方法提供了最直觀的趨勢指示。它能夠捕捉整體趨勢,但對短期波動比較敏感。
- 對數報酬率斜率:相較於簡單線性迴歸,此方法對價格變動的百分比較為敏感。它在處理長期趨勢和不同價格水平的資產比較時更有優勢。
- 多項式迴歸斜率:透過使用3階多項式,這種方法能夠捕捉更複雜的價格模式,例如加速上漲或減速下跌的趨勢。它對短期波動的反應比線性方法更敏感。
- 動態時間視窗斜率:此方法能夠根據市場波動性自動調整計算視窗。在高波動期,它提供了更敏感的訊號;在低波動期,則給予更平滑的趨勢指示。
從圖表中我們可以觀察到:
- 簡單線性迴歸斜率和對數收益率斜率提供了相似的趨勢訊號,但對數收益率斜率在處理大幅度價格變化時表現更穩定。
- 多項式迴歸斜率能夠捕捉更細微的趨勢變化,但也更容易受到短期波動的影響。
- 動態時間視窗斜率在不同市場條件下都表現良好,能夠及時捕捉趨勢變化,同時在低波動期提供更平滑的訊號。
在實際應用中,選擇哪一種方法取決於特定的交易策略和市場環境。例如:
- 對於長期投資者,對數收益率斜率可能更有價值,因為它能更好地反映長期趨勢。
- 對於短期交易者,多項式迴歸斜率或動態時間視窗斜率可能更有用,因為它們能夠更快地捕捉趨勢變化。
- 對於波動性交易策略,動態時間視窗斜率可能是最佳選擇,因為它能夠自動適應不同的市場條件。
需要注意的是,沒有一種方法是完美的。在實際交易中,我通常會結合多種方法,並與其他技術指標一起使用,以獲得更全面的市場視角。例如,可以使用簡單線性迴歸斜率來確定整體趨勢,然後使用動態時間視窗斜率來優化入場和出場時機。
儘管我們已經探討了幾種高階斜率運算方法,但金融市場分析的世界遠不止於此。在接下來的文章中,我們將深入探討多時間框架斜率分析,這將有助於我們更好地理解不同時間尺度的市場動態。此外,我們還將討論如何將斜率分析與其他技術指標結合,創造強大的交易策略。最後,我們將探討斜率分析在實際交易中的應用,以及如何利用新興技術如機器學習來增強我們的分析能力。
⑤ 結語
透過本文的探討,我們深入了解了幾種高階斜率計算方法,包括對數殖利率斜率、多項式迴歸斜率和動態時間視窗斜率。這些方法為我們提供了應對金融市場複雜性的強大工具。
回顧主要觀點:
- 對數報酬率斜率在處理長期趨勢和不同價格水準的資產比較時具有優勢。
- 多項式迴歸斜率能捕捉更複雜的市場模式,如加速或減速趨勢。
- 動態時間窗口斜率可以自動適應不同的市場波動條件,提供更靈活的分析。
基於這些認識,我為讀者提供以下實用建議:
- 根據您的交易時間框架選擇合適的斜率計算方法。長期投資者可能更適合使用對數收益率斜率,而短期交易者可能受益於動態時間窗口方法。
- 不要依賴單一方法。結合多種斜率運算技術可以提供更全面的市場洞察。
- 將斜率分析與其他技術指標結合使用,例如移動平均線或相對強弱指數(RSI),以獲得更可靠的交易訊號。
- 在實際應用中,持續監控和調整您的分析參數,以適應不斷變化的市場條件。
- 始終記住進行適當的風險管理。即使是最先進的分析方法也不能保證百分之百的準確性。
深度洞察:
這些高階斜率運算方法不僅提高了我們分析市場趨勢的能力,也反映了金融市場分析正在朝著更精細和動態的方向發展。它們代表了技術分析與統計、數學的深度融合,為量化交易策略的發展開闢了新的可能性。
展望未來,我預見這個領域將持續快速發展。機器學習和人工智慧技術的應用可能會帶來更智慧、更自適應的斜率運算方法。同時,大數據分析的進步可能使我們能夠在更廣泛的市場背景下解釋斜率訊號。
我鼓勵大家嘗試將這些方法應用到自己的交易分析中。開始可以從簡單的回測開始,逐步增加複雜性。記住,最好的學習方式是透過練習和不斷調整。
最後,我想聽聽您的想法。您是否已經在使用某些斜率分析方法?您遇到了哪些挑戰?或者您對這些方法有什麼新的見解?請在評論區分享您的經驗和問題,讓我們一起探討和學習。金融市場分析是一個不斷演進的領域,只有透過持續學習和交流,我們才能在這個充滿挑戰的市場中保持競爭力。
在下一篇文章中,我們將深入探討'多時間框架斜率分析:整合短期和長期趨勢'這個主題。我們將學習如何在不同時間尺度上應用斜率分析,並如何整合這些資訊來做出更明智的交易決策。敬請期待! "







