Decoding Slopes: Unveiling Mathematical Secrets of Market Trends

As a financial professional and financial self-publisher dedicated to the study and practice of quantitative trading, I am often asked, ‘How do I quickly determine market trends?’ Today, I'm going to reveal a powerful yet simple tool - slope. This mathematical concept is not only the cornerstone of trend analysis, it's also the magical key to the pulse of the market. Let's explore how slope can help us take direction in the financial ocean.

① The Mathematical Nature of Slope: Quantification of a Linear Relationship

Slope, a seemingly simple mathematical concept, plays a crucial role in financial market analysis. Based on my years of practice and observation in the quantitative trading market, I have found that many investors' understanding of slope is limited to secondary school maths textbooks, without realising its powerful application in the financial field.

Let's start with the most basic definition: slope describes the ‘steepness’ of a straight line. Mathematically, it is expressed as the change in the y-axis divided by the change in the x-axis. The formula is:

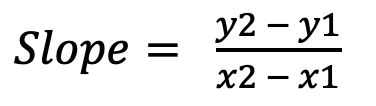
This simple formula has far-reaching implications in the financial markets. Imagine if the y-axis represents the price of an asset and the x-axis represents time, then the slope is a direct reflection of how quickly the price is changing over time. A positive slope implies an uptrend, a negative slope indicates a downtrend, and the greater the absolute value of the slope, the stronger the trend.

In my many years of trading, I have found that traders who are able to accurately identify market trends often have one thing in common: they are very sensitive to slope. They may not talk about the term ‘slope’ directly, but their method of analysis is essentially calculating and comparing the rate of price change of different assets over time.

While this basic concept may seem simple, the calculation and application of slope in complex financial markets can become quite complex. In our next article, we will delve into more advanced methods of calculating slope to deal with the non-linearity and high volatility of financial markets.

② The concept of slope in financial markets: an intuitive understanding of the rate of price change

In financial markets, slope is not just an abstract mathematical concept, it has a very intuitive and practical meaning. As a long-time quantitative trading professional, I have found that applying the concept of slope to everyday market analysis can greatly improve our ability to judge market movements.

Imagine you are looking at the price chart of a stock. When the price line shows a steep uptrend, this is actually an indication of a high positive slope. It means that in a short period of time, the price is rising fast. On the contrary, if the price line is almost horizontal, it is a slope close to zero, indicating little price change.

In my trading experience, I have found that slope can help:

• Identify trend strength: the greater the absolute value of the slope, the stronger the trend.
• Determine trend change: a change in slope from positive to negative or from negative to positive often means a trend reversal.
• Comparing different assets: By comparing the slopes of different assets, we can identify the strongest performing investment opportunities.

For example, let's say we observe that the price slope of stock A over the past month is 0.5, while the slope of stock B is 0.2. This tells us that stock A has risen faster than stock B. This could mean that stock A has risen faster than stock B. This could mean that stock A has risen faster than stock B. As an investor, this could mean that A-Shares currently have stronger upside momentum.

However, it is important to note that a high slope does not always mean a good investment opportunity. Sometimes, too high a slope can signal that prices have risen too fast and there is a risk of a pullback. This is why we need to combine it with other analytical tools to fully assess the market situation.

As our understanding of slope deepens, we will look at how we can combine slope analysis with other technical indicators and even use machine learning to enhance our analysis in future articles.

③ Basic Slope Calculation Methods

There are several commonly used slope calculation methods in financial market analysis. As a long-time quantitative trading professional, I have found that different methods have their own advantages and are applicable to different analysis scenarios. Let's explore three basic slope calculation methods.

3.1 Simple Linear Regression

Simple linear regression is a statistical method used to find the straight line that best represents a set of data points. In financial analysis, we often use it to calculate the slope of a price trend.

Method:

• Collect price data over a period of time.
• Find the line of best fit using the least squares method.
• The slope of that line is the slope of the price trend we are looking for.

Advantages:

• Considers all data points, reducing the impact of outliers.
• Provides a good estimate of the overall trend.

Disadvantages:

• Relatively complex to calculate.
• May not be sensitive enough to react to recent price changes.

3.2 Point-to-Point Method

The point-to-point method is the simplest and most straightforward method of calculating the slope. It only considers prices at the start and end points.

Method:

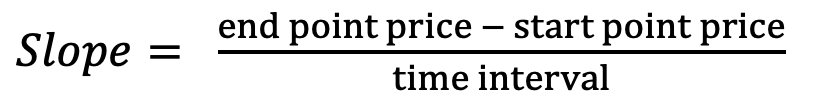
Advantages:

• Calculation is simple and fast.
• Intuitively reflects the overall price change.

Disadvantages:

• Ignores intermediate price fluctuations.
• Easily affected by the choice of starting and ending points.

3.3 Moving Average Slope

The Moving Average Slope method combines a moving average with a slope calculation and is one of the methods I personally use the most.

Method:

• Calculate two moving averages with different periods (e.g. 10-day and 20-day).
• Calculate the slope between these two moving averages.

Pros:

• Reduces the impact of short-term fluctuations and provides a smoother view of the trend.
• The moving average period can be adjusted to accommodate different trading cycles.

Disadvantages:

• Some lag exists.
• May not be responsive enough in highly volatile markets.

In practice, I often use a combination of these methods. For example, simple linear regression is used on daily charts to determine medium-term trends, while moving average slopes are used on hourly charts to find short-term trading opportunities. The point-to-point rule is often used to quickly assess the relative strengths and weaknesses of different assets.

Remember, no one method is perfect. The key is to understand the characteristics of each method and to be flexible in applying them to specific market conditions and trading objectives.

These basic methods provide a good starting point, but in actual trading we may need more sophisticated techniques to deal with the complexity of the market. In subsequent articles in the series, we will look at how to deal with non-linear trends and how to apply slope analysis in multiple time frames.

④ Application of Slope in Different Financial Markets

As a quantitative trading expert with experience in multiple financial markets, I have found that slope analysis has unique and powerful applications in different markets. Let's explore how slope works in the stock, forex and commodity markets.

4.1 Stock Market: Trend Strength Indicator

In the stock market, slope is a powerful tool for measuring trend strength.

Ways to apply it:

• Individual stock trend analysis: Calculating the slope of an individual stock's price can provide a visual indication of how fast it is rising or falling.
• Sector Comparison: Comparing the slopes of different sector indices can help us identify the strongest sectors.
• Momentum strategy: selecting stocks with the highest slope to invest in, using the principle of price inertia.

Example:

Suppose we compare the slopes of technology and financial stocks. If it is found that the slope of technology stocks is significantly higher than that of financial stocks, this could mean that the technology sector is in a stronger uptrend.

4.2 The foreign exchange market: speed of exchange rate movements

The foreign exchange market is the largest and most active financial market in the world and slope analysis has a unique application here.

Ways to apply it:

• Trend Strength Comparison: Compare the slopes of different currency pairs to identify the strongest and weakest currencies.
• Breakout Confirmation: Use the change in slope to confirm the validity of a price breakout.
• Relative Strength Analysis: assesses the overall strength of a currency by comparing its slope against different rival currencies.

Example:

If we observe a positive slope for the EURUSD and a negative slope for the EURJPY, this may suggest an overall strength of the USD and a relative weakness of the JPY.

4.3 Commodity markets: price momentum measurement

In commodity markets, slope analysis can help us capture price momentum and seasonal patterns.

Ways to apply it:

• Momentum analysis: uses slope to measure how fast commodity prices are rising or falling.
• Seasonal pattern identification: Identify seasonal price patterns by comparing slopes over different periods.
• Supply and Demand Determination: changes in slope may reflect changes in supply and demand.

Example:

In the crude oil market, if we find that the slope of the crude oil price always rises significantly in specific months of the year, this may reflect a seasonal pattern of increased demand.

In actual trading, I often use slope analysis in conjunction with other technical indicators. For example, in the stock market, I might combine the Relative Strength Indicator (RSI) with slope analysis to look for overbought or oversold opportunities. In the forex market, I might use slope to confirm signals generated by moving average crossovers.

Remember, while slope analysis is powerful, it is only one analytical tool among many. Successful trading strategies often require a combination of factors, including fundamental analysis, technical indicators and market sentiment.

Whilst we have seen the application of slope analysis in different markets, you may ask: how can you effectively apply this knowledge in an actual trading strategy? We will explore this in more detail in future articles, including how to build and optimise a slope-based trading system.

⑤ Hands-on example: calculating and visualising price slopes of different assets using Python

As a professional who is both a quantitative trader and an avid financial self-trader, I often stress the importance of combining theory and practice. Today, I'm going to show you how to calculate and visualise price slopes of different assets through a practical Python case study.

First, let's prepare the necessary Python libraries and data:

                                 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# Assume we already have a DataFrame with the date and closing price
data_dir = 'data'
file_path = f"{data_dir}/asset_prices.csv"
df = pd.read_csv(file_path, parse_dates=['Date'])



# Set the Date column as an index

df.set_index('Date', inplace=True)



# Make sure the data is sorted by date

df.sort_index(inplace=True)

Now, let's define a function to calculate the slope:

                                   
# Calculate the slope function
def calculate_slope(data, window=30):
    slopes = [np.nan] * (window - 1) 
    
    # add NaN value to the beginning
    for i in range(len(data) - window + 1): 
        y = data[i:i+window]
        x = np.arange(window)
        slope, _ = np.polyfit(x, y, 1)
        slopes.append(slope)
    return slopes

# Calculate slopes for both assets
df['Slope1'] = calculate_slope(df['Asset1'])
df[‘Slope2’] = calculate_slope(df['Asset2'])

# Print basic information about the dataset
print(df.info())
print('\nFirst few rows of the dataset:')
print(df.head())

Next, we'll graph the price and slope:

                                    
# visualise the data
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), sharex=True)

# Plot asset prices
ax1.plot(df.index, df['Asset1'], label='Asset1')
ax1.plot(df.index, df['Asset2'], label='Asset2')
ax1.set_title(‘Asset Prices’)
ax1.legend()

# plot the slope
ax2.plot(df.index, df['Slope1'], label='Slope of Asset1')
ax2.plot(df.index, df['Slope2'], label='Slope of Asset2')
ax2.set_title('Price Slopes (30-day window)')
ax2.axhline(y=0, colour='r', linestyle='--')
ax2.legend()

# Adjust the x-axis labels
plt.xticks(rotation=45)
plt.xlabel('Date')

# Adjust the layout
plt.tight_layout()
plt.show()

# Save processed data (optional)
df.to_csv(f'{data_dir}/processed_asset_prices.csv')
print(f 'Processed data saved to {data_dir}/processed_asset_prices.csv')

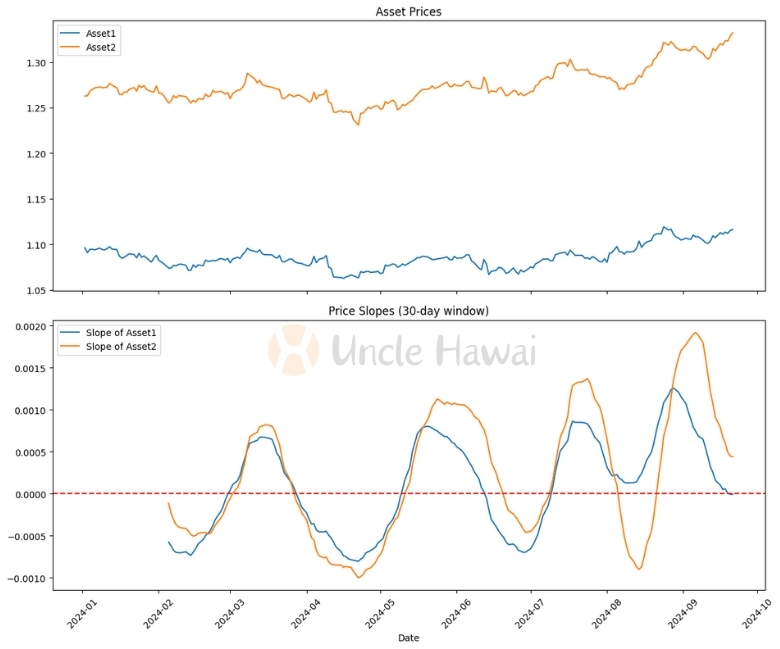
Slope of Asset Prices

This example shows how to calculate and visualise the slope of an asset price. We can visualise this by looking at the slope graph:

• A positive slope indicates an upward trend and a negative slope indicates a downward trend.
• The greater the absolute value of the slope, the stronger the trend.
• Changes in slope can help us identify turning points in a trend.

In real trading, I often use a similar method to compare the performance of different assets. For example, if I find that the slope of one asset is consistently higher than others, this may suggest a strong uptrend that deserves further attention.

I will also combine other technical indicators such as moving averages or the Relative Strength Indicator (RSI) to confirm the results of the slope analysis. Remember, no single indicator is perfect, and a comprehensive analysis is the key to developing a solid trading strategy.

This simple Python example is just the tip of the iceberg. In future articles, we will look at how we can use more advanced programming techniques, or even machine learning algorithms, to enhance our slope analysis.

⑥ Limitations and caveats of slope analysis

As a long-time quantitative trading and financial analysis professional, I am well aware that every analysis method has its strengths and limitations. Slope analysis, while powerful, is no exception. In this section, I will share some key things to keep in mind when using slope analysis.

6.1 Time Frame Sensitivity

The results of slope analysis are highly dependent on the time frame chosen. Slopes in the short term may fluctuate dramatically due to market noise, while long-term slopes may ignore important short-term trend changes.

Caution:

• Choose the appropriate time frame for your trading strategy.
• Consider using slopes from multiple time frames for cross-validation.

6.2 Lag

Slope analysis, especially slope calculated using moving averages, has a certain lag. This means that it may give signals after the trend has already started to change.

Caveat:

• Balance the lag of slope analysis with other leading indicators.
• Use shorter-term slopes to capture more timely trend changes.

6.3 Impact of Market Conditions

Slope analysis performs best in markets with a clear trend, but may produce misleading signals in oscillating markets or high volatility environments.

Caution:

• Assess current market conditions before using slope analysis.
• In oscillating markets, consider combining other technical analysis tools such as support and resistance levels.

6.4 Overfitting Risk

When optimising parameters for slope calculations, it is easy to fall into the trap of overfitting, where parameters perform well on historical data but fail in future markets.

Caution:

• Use sufficiently long historical data for backtesting.
• Use methods such as walk-forward optimisation to reduce the risk of overfitting.

6.5 Ignoring fundamentals

Pure reliance on technical indicators such as slope may ignore important fundamentals such as company earnings reports, economic data or geopolitical events.

Caveat:

• Combine slope analysis with fundamental analysis.
• Pay attention to significant events or announcements that may affect the slope.

6.6 Applicability to Different Asset Classes

Slope analysis may require different methods of interpretation and application in different asset classes. For example, seasonal factors in commodity markets may lead to cyclical slope changes.

Caveat:

• Adjust the parameters and methods of interpretation of slope analysis for different asset classes.
• Consider asset-specific influences, such as dividend policies for equities or interest rate differentials for foreign exchange.

Despite these limitations of slope analysis, don't be discouraged. In our next article, we will delve into how to overcome these challenges, including the use of more advanced slope calculation methods to cope with the non-linearity and high volatility of markets.

⑦ Conclusion

Slope analysis, as the mathematical foundation for the study of financial market trends, provides us with a powerful and intuitive tool to understand and predict market movements. Through this paper, we have provided insights into the mathematical nature of slope, its application in financial markets, and different methods of calculation.

Review our main points:

• Slope is not just a mathematical concept; it directly reflects the speed and direction of asset price changes.
• Different methods of slope calculation, such as simple linear regression, point-to-point method and moving average slope, each have their own advantages, disadvantages and scenarios of application.
• Slope analysis has a wide range of applications in the stock, forex and commodity markets, helping us to identify trend strength and compare the performance of different assets.
• With Python, we can easily calculate and visualise the slope of an asset's price, providing data to support investment decisions.
• Although powerful, slope analysis has its limitations, such as timeframe sensitivity and lag, and care needs to be taken when using it.

Based on these realisations, I offer readers the following practical advice:

• Combine slope analysis with other technical indicators and fundamental analysis to gain more comprehensive market insights.
• Experiment with slope analysis using different time frames to find the setup that best suits your trading style.
• Instead of using slope signals in isolation, use them as an important reference in your decision-making process in real trading.
• Keep learning and practising to optimise your slope analysis strategy through backtesting and simulated trading.
• Remain vigilant and keep an eye on market changes and unusual events that may affect the effectiveness of slope analysis.

Looking ahead, there is still a lot of room for the application of slope analysis in the financial markets. With advances in machine learning and artificial intelligence technology, we may see more sophisticated and accurate models for slope analysis. This may include adaptive slope algorithms that can automatically adjust parameters based on market conditions, or multi-dimensional slope models that incorporate big data analytics.

As participants in the financial markets, we should remain open and learning, constantly exploring and optimising our analytical tools and methods. Slope analysis opens a window to understanding market trends, but the real wisdom in investing lies in how to use these tools flexibly and combine them with our deep understanding of the market.

I hope this article has provided valuable insights into your investment journey. The financial markets are always full of challenges and opportunities, and mastering tools like slope analysis will help you make smarter decisions in this complex environment.

Finally, I invite you to share your experiences or any questions you may have about using slope analysis. Have you applied slope analysis in your own trading? What challenges have you encountered? Let's discuss and improve our investing skills together. Remember, learning and adapting never stops in the financial markets. We wish you success on your investing journey!

In this article, we laid the foundation for understanding slope analysis. But that was just the beginning. In our next article, Slope Advance: Navigating the Complexities of Financial Markets, we'll delve into more advanced slope techniques, including how to deal with non-linear trends and high volatility markets. We will also discuss how to combine slope analysis with other technical indicators to create even more powerful analytical tools. Stay tuned!