全方位斜率(上):掌握跨时间跨市场的趋势洞察
[免责声明] 本文仅供教育和信息目的,不构成投资建议。读者在做出任何投资决定前应咨询合格的金融专业人士。
在量化交易领域深耕多年,我发现市场趋势犹如一条奔腾的河流,有主流,也有支流。要全面把握市场动态,单一时间框架或单一市场的分析往往不够。今天,让我们一起探讨如何通过多维度斜率分析,在不同时间尺度和市场之间寻找趋势的共鸣。
① 时间框架的本质:从分钟到月度的斜率差异
作为一个长期从事量化交易研究的分析师,我常常被问到:"为什么同一支股票,在不同时间框架下的趋势看起来如此不同?"这个问题引出了我们今天要深入探讨的第一个主题:时间框架的本质。
在前两篇文章中,我们详细讨论了斜率的基本概念和高级计算方法。今天,我们要将这些知识应用到更广阔的视角中。不同时间框架下的斜率差异,实际上反映了市场参与者在不同时间尺度上的行为特征。
让我们通过一个具体的例子来理解这一点:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def calculate_slopes_multiple_timeframes(price_data, timeframes=['1H', '4H', '1D']):
"""
计算不同时间框架下的斜率
参数:
price_data: 原始价格数据(假设为分钟级别)
timeframes: 需要计算的时间框架列表
"""
results = {}
for tf in timeframes:
# 重采样数据
resampled = price_data.resample(tf).agg({
'open': 'first',
'high': 'max',
'low': 'min',
'close': 'last'
})
# 计算斜率(使用20个周期的窗口)
slopes = pd.Series(index=resampled.index)
window = 20
for i in range(window, len(resampled)):
y = resampled['close'].iloc[i-window:i]
x = np.arange(window)
slope, _ = np.polyfit(x, y, 1)
slopes.iloc[i] = slope
results[tf] = slopes
return results
这个函数帮助我们理解同一市场在不同时间框架下的斜率特征。有趣的是,我们经常发现:
- 短期时间框架(如分钟级别)的斜率波动更加剧烈,反映了市场的短期噪音。
- 中期时间框架(如小时级别)的斜率更能体现当前的主导趋势。
- 长期时间框架(如日线、周线)的斜率则展示了市场的基本面走势。
然而,这些不同时间框架的斜率并非孤立存在。正如河流中的支流最终汇入主流,不同时间框架的趋势也存在着内在的联系。在下一节中,我们将探讨如何协调和整合这些不同时间尺度的信息。
② 多时间框架斜率分析方法
在理解了不同时间框架的特性后,关键问题是如何有效地整合这些信息。这就像观察一幅画,我们既需要看到整体构图(长期趋势),又要注意局部细节(短期波动)。
2.1 时间框架协调:确保数据一致性
首先,让我们看看如何确保不同时间框架数据的一致性:
def align_timeframe_data(hourly_data, timeframes=['1h', '4h', '1d']):
"""
协调不同时间框架的数据,以小时数据为基础
参数:
hourly_data: 小时级基础数据('1H')
timeframes: 需要分析的更大时间框架列表
返回:
DataFrame: 包含所有时间框架斜率的对齐数据
"""
aligned_slopes = {}
# 计算更大时间框架的斜率
for tf in timeframes:
# 重采样数据
resampled = hourly_data.resample(tf).agg({
'close': 'last',
'volume': 'sum'
}).dropna()
# 计算标准化斜率
slopes = calculate_normalized_slope(resampled['close'], window=20)
# 将斜率数据对齐到小时框架
if tf == '1h':
aligned_slopes[tf] = slopes
else:
# 将斜率数据对齐到小时框架
aligned_slopes[tf] = slopes.reindex(aligned_slopes['1h'].index, method='ffill')
return pd.DataFrame(aligned_slopes)
def calculate_normalized_slope(prices, window=20):
"""
计算标准化斜率
"""
slopes = pd.Series(index=prices.index)
price_std = prices.rolling(window).std()
for i in range(window, len(prices)):
y = prices.iloc[i-window:i]
x = np.arange(window)
slope, _ = np.polyfit(x, y, 1)
# 使用标准差标准化斜率
slopes.iloc[i] = slope / price_std.iloc[i] if price_std.iloc[i] != 0 else 0
return slopes
# 使用示例
# 获取对齐的斜率数据
aligned_slopes = align_timeframe_data(hourly_data)
print(f"数据形状: {aligned_slopes.shape}")
print("\n每个时间框架的非空值数量:")
print(aligned_slopes.count())
# 显示出5月份对齐的斜率数据
monthly_mask = (aligned_slopes.index.year == 2024) & (aligned_slopes.index.month == 5)
aligned_slopes[monthly_mask].plot()
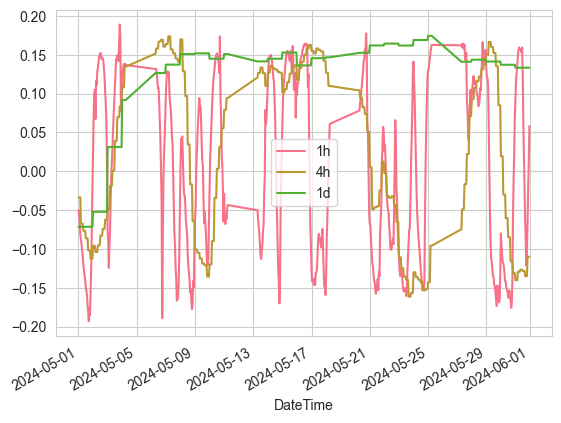
这个方法的关键在于:
- 使用标准化处理,使不同时间框架的斜率具有可比性
- 通过重采样和数据对齐,确保不同时间框架的数据在时间上同步
- 考虑了成交量信息,增加分析维度
2.2 斜率叠加技术:综合不同时间尺度的趋势
现在,让我们看看如何将不同时间框架的斜率信息整合起来:
def composite_slope_indicator(aligned_slopes, weights={'1h': 0.3, '4h': 0.3, '1d': 0.4}):
"""
创建综合斜率指标
参数:
aligned_slopes: 对齐后的各时间框架斜率数据
weights: 各时间框架的权重
"""
composite = pd.Series(0, index=aligned_slopes.index)
for tf, weight in weights.items():
composite += aligned_slopes[tf] * weight
return composite
# 获取组合的斜率数据
composite_slope = composite_slope_indicator(aligned_slopes)
# 显示出5月份的组合斜率数据
composite_slope[monthly_mask].plot()
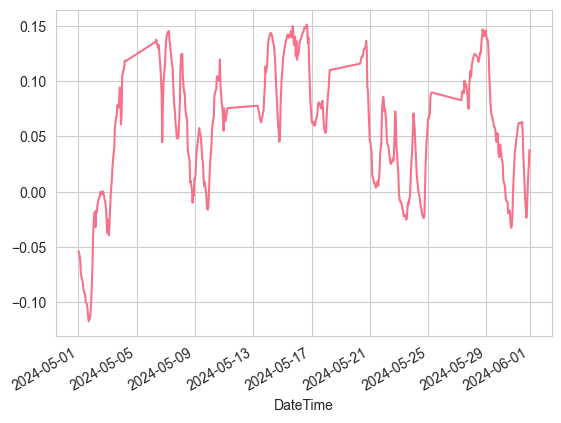
这个综合指标有几个显著特点:
- 权重可调:可以根据交易策略调整不同时间框架的权重
- 信号确认:多个时间框架的趋势一致时,信号更可靠
- 冲突识别:当不同时间框架的趋势出现分歧时,提供预警
在实践中,我发现这种多时间框架的分析方法能够帮助我们:
- 更好地识别主导趋势
- 找到更合适的入场点
- 降低假信号的影响
但需要注意的是,随着分析维度的增加,我们也面临着更复杂的信号解释问题。这个挑战将在本文后面的部分详细讨论。值得一提的是,在下一篇文章中,我们将探讨如何将这些分析转化为具体的交易策略。
③ 跨市场斜率相关性
在金融市场中,不同市场之间的联系就像是一张无形的网。作为一个资深量化分析师,我发现斜率分析在揭示这些市场关联性方面有着独特的优势。
3.1 外汇对与商品的斜率关系
让我们先来看一个经典的例子 - EUR/USD与黄金价格的关系:
def analyze_cross_market_slopes(market1_data, market2_data, window=30):
"""
分析两个市场之间的斜率相关性
参数:
market1_data, market2_data: 两个市场的价格数据
window: 计算斜率和相关性的窗口大小
"""
# 计算两个市场的标准化斜率
slopes1 = calculate_normalized_slope(market1_data, window)
slopes2 = calculate_normalized_slope(market2_data, window)
# 将斜率数据合并成DataFrame并对齐数据
combined_slopes = pd.DataFrame({
'slopes1': slopes1,
'slopes2': slopes2
})
# 删除含有空值的行
combined_slopes = combined_slopes.dropna()
# 打印调试信息
print("\n数据处理前:")
print("Slopes1 shape:", slopes1.shape)
print("Slopes2 shape:", slopes2.shape)
print("NaN in slopes1:", slopes1.isna().sum())
print("NaN in slopes2:", slopes2.isna().sum())
print("\n数据处理后:")
print("Combined shape:", combined_slopes.shape)
print("NaN in combined data:", combined_slopes.isna().sum().sum())
# 计算滚动相关性
correlation = combined_slopes['slopes1'].rolling(window).corr(combined_slopes['slopes2'])
# 计算领先-滞后关系
lead_lag = pd.DataFrame(index=combined_slopes.index)
for lag in range(-5, 6):
if lag > 0:
shifted_slopes2 = combined_slopes['slopes2'].shift(lag)
corr = combined_slopes['slopes1'].rolling(window).corr(shifted_slopes2)
else:
shifted_slopes1 = combined_slopes['slopes1'].shift(-lag)
corr = shifted_slopes1.rolling(window).corr(combined_slopes['slopes2'])
lead_lag[f'lag_{lag}'] = corr
print("\n结果统计:")
print("Correlation NaN count:", correlation.isna().sum())
print("Total periods in correlation:", len(correlation))
return correlation, lead_lag
def visualize_cross_market_analysis(correlation, lead_lag):
"""
可视化跨市场分析结果
参数:
correlation: 相关性时间序列
lead_lag: 领先-滞后关系DataFrame
"""
# 创建带有共享x轴的子图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8), sharex=True)
# 绘制相关性时间序列
ax1.plot(range(len(correlation)), correlation.values, label='相关性')
ax1.set_title('斜率相关性随时间的变化')
ax1.axhline(y=0, color='r', linestyle='--', alpha=0.3)
ax1.grid(True)
ax1.set_ylabel('相关性')
# 设置第一个图的x轴刻度
n_ticks = 5 # 设置想要显示的刻度数量
step = len(correlation) // (n_ticks - 1)
tick_positions = np.arange(0, len(correlation), step)
tick_labels = correlation.index[::step]
ax1.set_xticks(tick_positions)
ax1.set_xticklabels(tick_labels, rotation=45)
# 绘制领先-滞后热图
im = ax2.imshow(lead_lag.T,
aspect='auto',
extent=[0, len(lead_lag), -5.5, 5.5],
cmap='RdBu_r',
interpolation='nearest')
# 设置第二个图的x轴刻度(与第一个图相同)
ax2.set_xticks(tick_positions)
ax2.set_xticklabels(tick_labels, rotation=45)
# 设置y轴标签
ax2.set_ylabel('领先/滞后周期')
ax2.set_title('领先-滞后关系分析')
# 添加颜色条
plt.colorbar(im, ax=ax2, label='相关性强度')
# 调整布局
plt.tight_layout()
return fig
def enhanced_visualize_cross_market_analysis(correlation, lead_lag,
title=None,
show_threshold=False,
threshold=0.5):
"""
增强版可视化函数
"""
# 创建带有共享x轴的子图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8), sharex=True)
if title:
fig.suptitle(title, y=1.02, fontsize=14)
# 绘制相关性时间序列
ax1.plot(range(len(correlation)), correlation.values, label='相关性')
ax1.set_title('斜率相关性随时间的变化')
ax1.axhline(y=0, color='r', linestyle='--', alpha=0.3, label='零线')
if show_threshold:
ax1.axhline(y=threshold, color='g', linestyle='--', alpha=0.3, label=f'阈值 ({threshold})')
ax1.axhline(y=-threshold, color='g', linestyle='--', alpha=0.3)
ax1.grid(True)
ax1.set_ylabel('相关性')
ax1.legend()
# 设置第一个图的x轴刻度
n_ticks = 5 # 设置想要显示的刻度数量
step = len(correlation) // (n_ticks - 1)
tick_positions = np.arange(0, len(correlation), step)
tick_labels = correlation.index[::step]
ax1.set_xticks(tick_positions)
ax1.set_xticklabels(tick_labels, rotation=45)
# 绘制领先-滞后热图
im = ax2.imshow(lead_lag.T,
aspect='auto',
extent=[0, len(lead_lag), -5.5, 5.5],
cmap='RdBu_r',
interpolation='nearest')
# 设置第二个图的x轴刻度(与第一个图相同)
ax2.set_xticks(tick_positions)
ax2.set_xticklabels(tick_labels, rotation=45)
# 设置y轴标签和刻度
ax2.set_ylabel('领先/滞后周期')
ax2.set_yticks(np.arange(-5, 6))
ax2.set_title('领先-滞后关系分析')
# 添加颜色条
cbar = plt.colorbar(im, ax=ax2)
cbar.set_label('相关性强度')
# 调整布局
plt.tight_layout()
return fig
# 获得两个品种的斜率相关性
correlation_analyze, analyze_lead_lag = analyze_cross_market_slopes(resampled_df1['close'], resampled_df2['close'])
# 只显示5月的相关性图表
monthly_mask3 = (correlation_analyze.index.year == 2024) & (correlation_analyze.index.month == 5)
analyze_lead_lag3 = (analyze_lead_lag.index.year == 2024) & (analyze_lead_lag.index.month == 5)
fig = visualize_cross_market_analysis(correlation_analyze[monthly_mask3], analyze_lead_lag[analyze_lead_lag3])
plt.show()
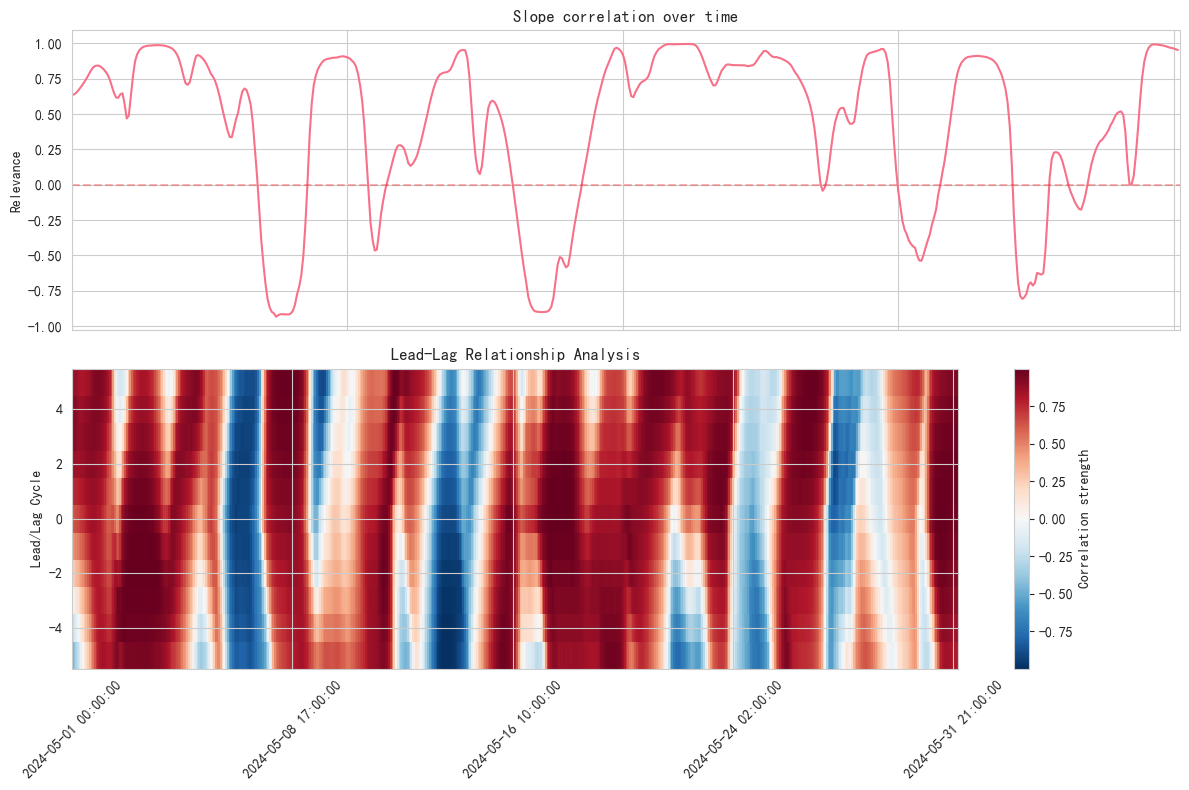
通过这个分析,我们可以发现一些有趣的现象:
- EUR/USD与黄金价格的斜率相关性往往在特定的市场环境下会显著增强
- 这种相关性可能存在领先-滞后关系,为预测提供了可能性
- 相关性的突然变化可能预示着市场环境的转变
3.2 股指与个股斜率的联系
在股票市场中,个股与大盘之间的斜率关系同样值得研究:
这种分析方法帮助我们:
- 识别个股的独特走势
- 发现潜在的alpha机会
- 优化投资组合的风险管理
值得注意的是,这些跨市场关系并非一成不变。在我们的下一篇文章中,我们将探讨如何将这些关系整合到实际的交易策略中。现在,让我们继续深入研究如何开发更复杂的多维度斜率指标。







