解密高级斜率:驾驭金融市场复杂性的利器
[免责声明] 本文仅供教育和信息目的,不构成投资建议。读者在做出任何投资决定前应咨询合格的金融专业人士。
在上一篇文章中,我们探讨了斜率分析的基础知识和简单应用。今天,我们将深入高级斜率计算方法。这个在金融市场分析中日益重要的工具。它不仅能帮助我们应对市场的复杂性,还能为投资决策提供更精准的指引。
① 对数收益率斜率及其优势
在金融市场分析中,对数收益率斜率是一个强大而又常被忽视的工具。与普通的价格斜率相比,对数收益率斜率有着显著的优势,特别是在处理长期趋势和不同价格尺度的资产时。
首先,让我们理解什么是对数收益率。对数收益率是指资产价格自然对数的变化。数学表达式为:
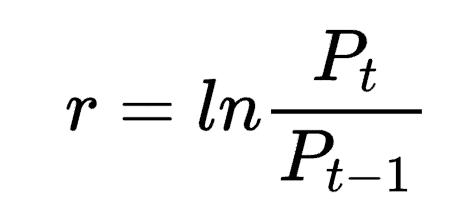
其中,r是对数收益率,Pt是当前价格,Pt-1是前一期价格。
对数收益率斜率的计算方法是对一段时间内的对数收益率进行线性回归,得到的斜率就是我们所需的对数收益率斜率。
对数收益率斜率的主要优势包括:
- 标准化:对数收益率可以标准化不同价格水平的资产,使得高价格和低价格的资产可以直接比较。
- 复利效应:对数收益率能更好地反映复利效应,这在长期分析中尤为重要。
- 对称性:对数收益率在正负方向上是对称的,这使得上涨和下跌的幅度更易比较。
- 稳定性:对数收益率通常比普通收益率更稳定,减少了极端值的影响。
让我们通过一个简单的Python示例来说明如何计算对数收益率斜率:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns
# 设置 seaborn 样式
sns.set_style("whitegrid") # 或者使用 "darkgrid", "white", "dark", "ticks"
# 创建画布和子图
fig, axes = plt.subplots(2, 1, figsize=(15, 12), sharex=True)
# 设置配色方案(可选)
sns.set_palette("husl")
# 原始价格图
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices')
axes[0].legend()
axes[0].grid(True)
# 对数收益率斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['log_slope'], label=f'{asset} Log Slope')
axes[1].set_title('Log Return Slopes')
axes[1].legend()
axes[1].grid(True)
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 调整x轴标签
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自动调整日期标签的格式
# 调整子图之间的间距
plt.tight_layout()
# 显示图形
plt.show()
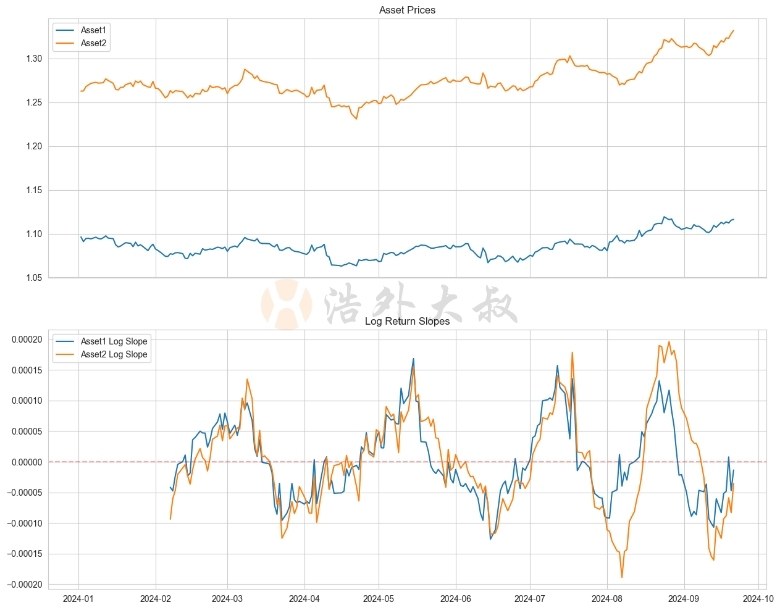
这个函数计算了一个滚动窗口内的对数收益率斜率。通过调整窗口大小,我们可以捕捉不同时间尺度的趋势。
在实际应用中,对数收益率斜率可以帮助我们识别长期趋势,比较不同资产类别的表现,甚至在跨市场分析中发挥作用。例如,当我们比较一个高价股票和一个低价股票的趋势时,对数收益率斜率可以提供更公平的比较基础。
然而,需要注意的是,对数收益率斜率虽然强大,但并非万能。在短期分析或高频交易中,普通价格斜率可能更直观。因此,选择合适的斜率计算方法应该根据具体的分析目的和时间范围来决定。
虽然对数收益率斜率提供了许多优势,但在多时间框架分析中如何有效应用这种方法呢?我们将在未来的文章中深入探讨这个问题,展示如何将不同时间尺度的斜率分析整合起来,以获得更全面的市场视角。
在下一节中,我们将探讨如何处理非线性趋势,这是金融市场中常见的复杂情况。通过多项式回归,我们可以捕捉更复杂的市场动态,为我们的分析工具箱增添新的利器。
② 非线性趋势和多项式回归
金融市场中的趋势往往不是简单的直线,而是呈现各种复杂的非线性模式。这就是为什么我们需要更高级的技术来捕捉这些复杂的市场动态。多项式回归就是这样一个强大的工具,它可以帮助我们模拟和分析非线性趋势。
多项式回归是线性回归的扩展,它使用多项式函数来模拟数据的曲线关系。一般形式为:
y = β₀ + β₁x + β₂x² + ... + βₙxⁿ + ε
其中,n是多项式的阶数,β是系数,ε是误差项。
在金融市场分析中,多项式回归可以帮助我们:
- 捕捉复杂的市场周期
- 识别潜在的反转点
- 更准确地预测短期和中期趋势
让我们通过一个Python示例来说明如何使用多项式回归分析市场趋势:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import seaborn as sns
def polynomial_regression_slope(prices, degree=2, window=30):
"""
使用多项式回归计算斜率
"""
# 预先创建存储结果的Series,填充NaN
slopes = pd.Series(np.nan, index=prices.index)
x = np.arange(window).reshape(-1, 1)
poly_features = PolynomialFeatures(degree=degree, include_bias=False)
x_poly = poly_features.fit_transform(x)
for i in range(window, len(prices)):
y = prices.iloc[i-window:i]
if not y.isna().any(): # 确保没有缺失值
model = LinearRegression()
model.fit(x_poly, y)
# 计算最后一点的斜率
last_x = x_poly[-1].reshape(1, -1)
slope = np.sum(model.coef_ * last_x * np.arange(1, degree+1))
slopes.iloc[i] = slope
return slopes
# 计算斜率
window = 30
results = {}
for asset in ['Asset1', 'Asset2']:
results[asset] = {
'poly_slope': polynomial_regression_slope(df[asset], degree=3, window=window),
}
# 设置 seaborn 样式
sns.set_style("whitegrid")
sns.set_palette("husl")
# 创建画布和子图
fig, axes = plt.subplots(2, 1, figsize=(15, 12), sharex=True)
# 原始价格图
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices', fontsize=12, pad=10)
axes[0].legend()
# 多项式回归斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['poly_slope'], label=f'{asset} Poly Slope')
axes[1].set_title('Polynomial Regression Slopes (Degree 3)', fontsize=12, pad=10)
axes[1].legend()
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 调整x轴标签
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自动调整日期标签的格式
# 调整子图之间的间距
plt.tight_layout()
# 显示图形
plt.show()
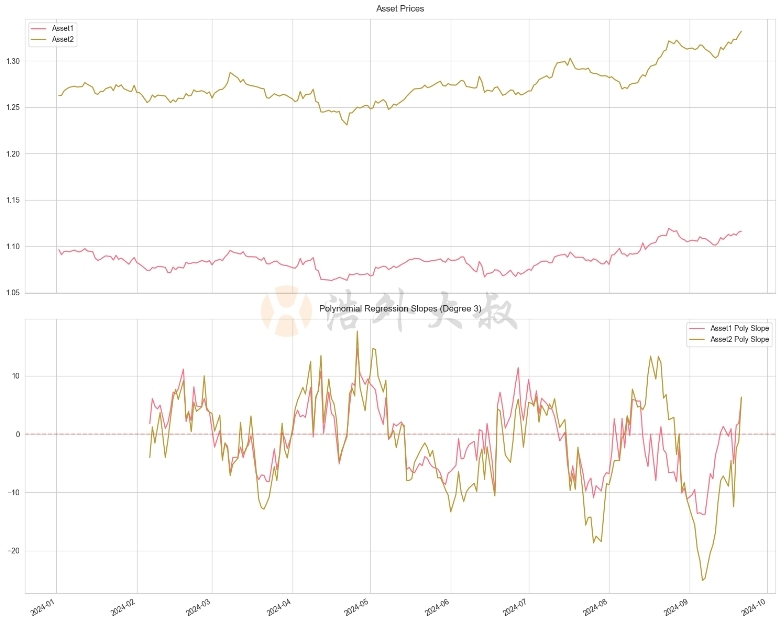
在这个例子中,我们使用了3阶多项式回归来计算斜率。这种方法可以捕捉更复杂的价格模式,比如加速上涨或减速下跌的趋势。
多项式回归的一个关键优势是它可以适应各种市场条件。例如,在牛市初期,我们可能会看到一个上凸的曲线,而在市场顶部附近,曲线可能会变得平缓或开始下弯。通过观察多项式回归的斜率变化,我们可以更早地识别这些潜在的市场转折点。
然而,使用多项式回归时也需要注意几个问题:
- 过拟合:高阶多项式可能会过度拟合数据,导致对噪音过于敏感。
- 参数选择:选择适当的多项式阶数和窗口大小至关重要。
- 计算复杂度:高阶多项式回归的计算量较大,可能不适合高频交易。
在实际应用中,我通常会结合使用不同阶数的多项式回归,以获得更全面的市场视角。例如,2阶多项式可以帮助识别整体趋势,而3阶或4阶多项式则可以捕捉更细微的市场动态。
在下一节中,我们将探讨如何使用动态时间窗口来进一步提高斜率计算的准确性和适应性。这种方法可以帮助我们更好地应对市场波动性的变化,为我们的分析提供更精确的工具。
③ 动态时间窗口在斜率计算中的应用
在金融市场分析中,固定时间窗口的斜率计算方法虽然简单直观,但往往难以适应市场波动性的变化。这就是为什么动态时间窗口在斜率计算中变得越来越重要。动态时间窗口可以根据市场条件自动调整,从而提供更准确和及时的趋势信号。
动态时间窗口的核心思想是根据市场的波动性来调整计算斜率所使用的时间窗口大小。在波动性较低的市场中,我们可以使用较大的时间窗口来减少噪音的影响;而在高波动性市场中,较小的时间窗口可以帮助我们更快地捕捉趋势变化。
以下是一个使用动态时间窗口计算斜率的Python示例:
import numpy as np
import pandas as pd
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import seaborn as sns
def dynamic_window_slope(prices, min_window=10, max_window=50, volatility_lookback=20):
"""
使用动态时间窗口计算斜率
参数:
prices: 价格序列
min_window: 最小窗口大小
max_window: 最大窗口大小
volatility_lookback: 计算波动率的回看期
"""
# 预先创建存储结果的Series,填充NaN
slopes = pd.Series(np.nan, index=prices.index)
# 计算波动率
returns = prices.pct_change()
volatility = returns.rolling(window=volatility_lookback).std()
# 处理极端值和缺失值
volatility = volatility.fillna(0) # 填充NA值
# 如果所有值都相同,直接使用最大窗口
if volatility.min() == volatility.max():
dynamic_window = pd.Series(max_window, index=prices.index)
else:
# 计算动态窗口大小
normalized_vol = (volatility - volatility.min()) / (volatility.max() - volatility.min())
dynamic_window = ((1 - normalized_vol) * (max_window - min_window) + min_window)
# 确保窗口大小在合理范围内
dynamic_window = dynamic_window.clip(min_window, max_window)
# 转换为整数
dynamic_window = dynamic_window.astype(int)
# 计算斜率
for i in range(max_window, len(prices)):
window = dynamic_window.iloc[i]
x = np.arange(window)
y = prices.iloc[i-window:i]
if not y.isna().any(): # 确保没有缺失值
try:
slope, _ = np.polyfit(x, y, 1)
slopes.iloc[i] = slope
except:
continue
return slopes
# 计算斜率
window = 30
results = {}
for asset in ['Asset1', 'Asset2']:
results[asset] = {
'dynamic_slope': dynamic_window_slope(df[asset])
}
# 设置 seaborn 样式
sns.set_style("whitegrid")
sns.set_palette("husl")
# 创建画布和子图
fig, axes = plt.subplots(2, 1, figsize=(15, 12), sharex=True)
# 原始价格图
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices', fontsize=12, pad=10)
axes[0].legend()
# 动态窗口斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['dynamic_slope'], label=f'{asset} Dynamic Slope')
axes[1].set_title('Dynamic Window Slopes', fontsize=12, pad=10)
axes[1].legend()
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 调整x轴标签
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自动调整日期标签的格式
# 调整子图之间的间距
plt.tight_layout()
# 显示图形
plt.show()
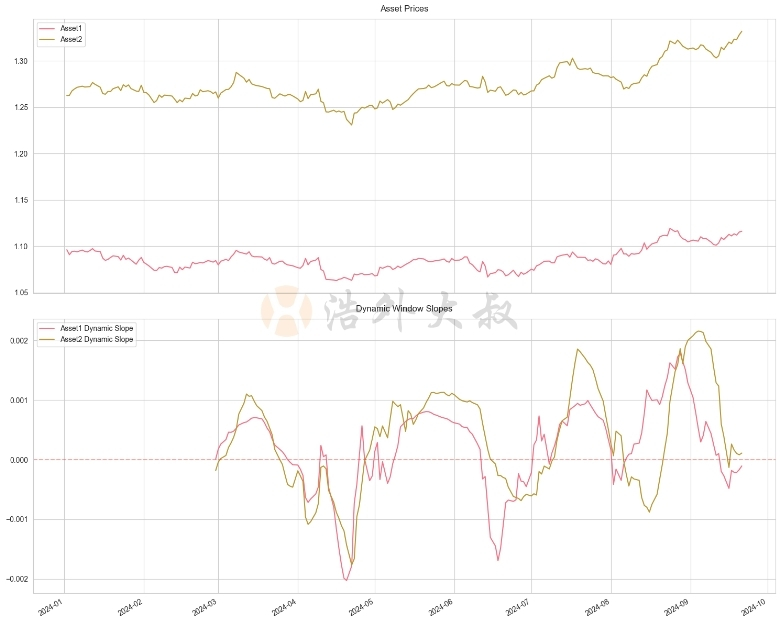
在这个例子中,我们根据市场的波动性动态调整时间窗口的大小。当波动性增加时,窗口变小,使得斜率计算更快响应市场变化;当波动性减小时,窗口变大,提供更平滑的趋势信号。
动态时间窗口方法的主要优势包括:
- 适应性强:能够自动适应不同的市场条件。
- 信号质量提升:在不同波动环境下提供更准确的趋势信号。
- 降低滞后性:在高波动期能更快捕捉趋势变化。
然而,使用动态时间窗口时也需要注意以下几点:
- 参数选择:最小和最大窗口大小以及波动性计算的回溯期需要谨慎选择。
- 计算复杂度:相比固定窗口,动态窗口方法的计算量较大。
- 过度敏感:在某些情况下可能会对短期波动过度敏感。
在实际应用中,我经常将动态时间窗口方法与其他技术指标结合使用。例如,可以将动态窗口斜率与相对强弱指数(RSI)或移动平均线结合,以获得更全面的市场视角。
这种方法特别适合那些波动性经常变化的市场,如外汇市场或某些高波动性的股票。通过动态调整分析的时间框架,我们可以更好地把握市场的脉搏,做出更明智的投资决策。
多项式回归为我们提供了处理非线性趋势的强大工具。然而,如何选择最佳的多项式阶数呢?在后续文章中,我们将探讨如何使用机器学习技术来自动优化这些参数,进一步提高我们的分析精度。
在下一节中,我们将通过一个具体的案例研究,比较不同斜率计算方法在股票趋势分析中的表现。这将帮助我们更好地理解这些方法的实际应用价值,并为选择适当的分析工具提供指导。
④ 案例研究:比较不同斜率计算方法在股票趋势分析中的表现
为了更好地理解不同斜率计算方法的实际应用价值,让我们通过一个具体的案例来比较它们在股票趋势分析中的表现。我们将使用历史数据作为例子,比较简单线性回归、对数收益率斜率、多项式回归斜率和动态时间窗口斜率这四种方法。
首先,让我们获取数据并实现这些方法:
# 简单线性回归斜率
def simple_slope(prices, window=30):
"""
使用简单线性回归计算斜率
参数:
prices: pandas Series, 价格序列
window: int, 计算斜率的窗口大小
返回:
pandas Series, 包含斜率值,索引与输入数据对应
"""
# 预先创建存储结果的Series,填充NaN
slopes = pd.Series(np.nan, index=prices.index)
# 准备用于回归的X值(时间索引)
x = np.arange(window)
# 计算斜率
for i in range(window, len(prices) + 1):
# 获取窗口内的价格数据
y = prices.iloc[i-window:i]
# 检查是否有缺失值
if not y.isna().any():
try:
# 使用 scipy.stats 的 linregress 计算斜率
slope, _, _, _, _ = stats.linregress(x, y)
slopes.iloc[i-1] = slope
except:
continue
return slopes
# 为两个资产计算不同类型的斜率
window = 30
results = {}
for asset in ['Asset1', 'Asset2']:
results[asset] = {
'simple_slope': simple_slope(df[asset], window),
'log_slope': log_return_slope(df[asset], window),
'poly_slope': polynomial_regression_slope(df[asset], degree=3, window=window),
'dynamic_slope': dynamic_window_slope(df[asset])
}
# 设置 seaborn 样式
sns.set_style("whitegrid")
sns.set_palette("husl")
# 创建画布和子图
fig, axes = plt.subplots(5, 1, figsize=(15, 12), sharex=True)
# 原始价格图
for asset in ['Asset1', 'Asset2']:
axes[0].plot(df.index, df[asset], label=asset)
axes[0].set_title('Asset Prices', fontsize=12, pad=10)
axes[0].legend()
# 简单斜率
for asset in ['Asset1', 'Asset2']:
axes[1].plot(df.index, results[asset]['simple_slope'], label=f'{asset} Simple Slope')
axes[1].set_title('Simple Slopes', fontsize=12, pad=10)
axes[1].legend()
axes[1].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 对数收益率斜率
for asset in ['Asset1', 'Asset2']:
axes[2].plot(df.index, results[asset]['log_slope'], label=f'{asset} Log Slope')
axes[2].set_title('Log Return Slopes', fontsize=12, pad=10)
axes[2].legend()
axes[2].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 多项式回归斜率
for asset in ['Asset1', 'Asset2']:
axes[3].plot(df.index, results[asset]['poly_slope'], label=f'{asset} Poly Slope')
axes[3].set_title('Polynomial Regression Slopes (Degree 3)', fontsize=12, pad=10)
axes[3].legend()
axes[3].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 动态窗口斜率
for asset in ['Asset1', 'Asset2']:
axes[4].plot(df.index, results[asset]['dynamic_slope'], label=f'{asset} Dynamic Slope')
axes[4].set_title('Dynamic Window Slopes', fontsize=12, pad=10)
axes[4].legend()
axes[4].axhline(y=0, color='r', linestyle='--', alpha=0.3) # 添加零线参考
# 调整x轴标签
plt.xticks(rotation=45)
fig.autofmt_xdate() # 自动调整日期标签的格式
# 添加总标题
fig.suptitle('Comparison of Different Slope Calculation Methods',
fontsize=14, y=1.02)
# 调整子图之间的间距
plt.tight_layout()
# 显示图形
plt.show()
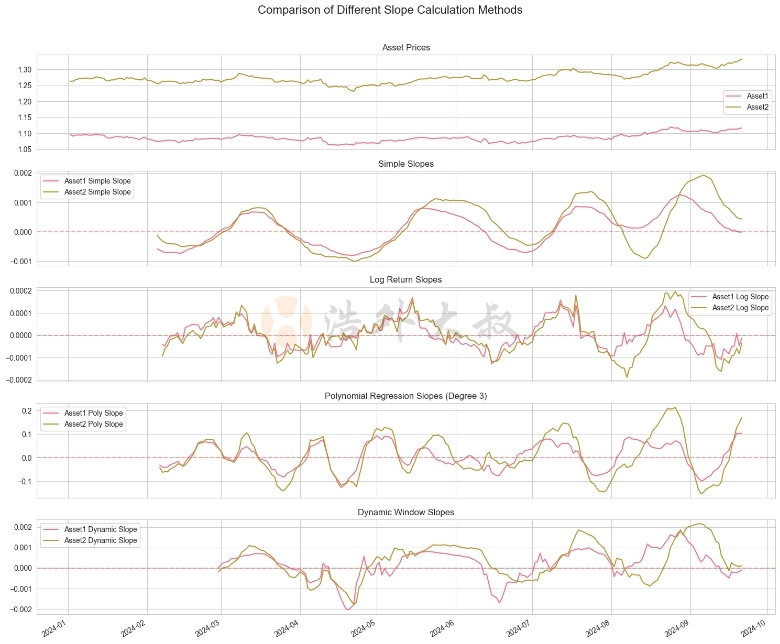
这段代码实现了四种不同的斜率计算方法,并将它们应用于苹果公司的股票数据。让我们分析一下每种方法的表现:
- 简单线性回归斜率:这种方法提供了最直观的趋势指示。它能够捕捉整体趋势,但对短期波动比较敏感。
- 对数收益率斜率:相比简单线性回归,这种方法对价格变化的百分比更敏感。它在处理长期趋势和不同价格水平的资产比较时更有优势。
- 多项式回归斜率:通过使用3阶多项式,这种方法能够捕捉更复杂的价格模式,如加速上涨或减速下跌的趋势。它对短期波动的反应比线性方法更敏感。
- 动态时间窗口斜率:这种方法能够根据市场波动性自动调整计算窗口。在高波动期,它提供了更敏感的信号;在低波动期,则给出更平滑的趋势指示。
从图表中我们可以观察到:
- 简单线性回归斜率和对数收益率斜率提供了相似的趋势信号,但对数收益率斜率在处理大幅度价格变化时表现更稳定。
- 多项式回归斜率能够捕捉更细微的趋势变化,但也更容易受到短期波动的影响。
- 动态时间窗口斜率在不同市场条件下都表现良好,能够及时捕捉趋势变化,同时在低波动期提供更平滑的信号。
在实际应用中,选择哪种方法取决于具体的交易策略和市场环境。例如:
- 对于长期投资者,对数收益率斜率可能更有价值,因为它能更好地反映长期趋势。
- 对于短期交易者,多项式回归斜率或动态时间窗口斜率可能更有用,因为它们能够更快地捕捉趋势变化。
- 对于波动性交易策略,动态时间窗口斜率可能是最佳选择,因为它能够自动适应不同的市场条件。
需要注意的是,没有一种方法是完美的。在实际交易中,我通常会结合多种方法,并与其他技术指标一起使用,以获得更全面的市场视角。例如,可以使用简单线性回归斜率来确定整体趋势,然后使用动态时间窗口斜率来优化入场和出场时机。
尽管我们已经探讨了几种高级斜率计算方法,但金融市场分析的世界远不止于此。在接下来的文章中,我们将深入探讨多时间框架斜率分析,这将帮助我们更好地理解不同时间尺度的市场动态。此外,我们还将讨论如何将斜率分析与其他技术指标结合,创建强大的交易策略。最后,我们将探索斜率分析在实际交易中的应用,以及如何利用新兴技术如机器学习来增强我们的分析能力。
⑤ 结语
通过本文的探讨,我们深入了解了几种高级斜率计算方法,包括对数收益率斜率、多项式回归斜率和动态时间窗口斜率。这些方法为我们提供了应对金融市场复杂性的强大工具。
回顾主要观点:
- 对数收益率斜率在处理长期趋势和不同价格水平的资产比较时具有优势。
- 多项式回归斜率能捕捉更复杂的市场模式,如加速或减速趋势。
- 动态时间窗口斜率可以自动适应不同的市场波动条件,提供更灵活的分析。
基于这些认识,我为读者提供以下实用建议:
- 根据您的交易时间框架选择合适的斜率计算方法。长期投资者可能更适合使用对数收益率斜率,而短期交易者可能受益于动态时间窗口方法。
- 不要依赖单一方法。结合多种斜率计算技术可以提供更全面的市场洞察。
- 将斜率分析与其他技术指标结合使用,如移动平均线或相对强弱指数(RSI),以获得更可靠的交易信号。
- 在实际应用中,持续监控和调整您的分析参数,以适应不断变化的市场条件。
- 始终记住进行适当的风险管理。即使是最先进的分析方法也不能保证百分之百的准确性。
深度洞察:
这些高级斜率计算方法不仅提高了我们分析市场趋势的能力,还反映了金融市场分析正在向更加精细和动态的方向发展。它们代表了技术分析与统计学、数学的深度融合,为量化交易策略的发展开辟了新的可能性。
展望未来,我预见这个领域将继续快速发展。机器学习和人工智能技术的应用可能会带来更智能、更自适应的斜率计算方法。同时,大数据分析的进步可能使我们能够在更广泛的市场背景下解释斜率信号。
我鼓励大家尝试将这些方法应用到自己的交易分析中。开始可以从简单的回测开始,逐步增加复杂性。记住,最好的学习方式是通过实践和不断调整。
最后,我想听听您的想法。您是否已经在使用某些斜率分析方法?您遇到了哪些挑战?或者您对这些方法有什么新的见解?请在评论区分享您的经验和问题,让我们一起探讨和学习。金融市场分析是一个不断演进的领域,只有通过持续学习和交流,我们才能在这个充满挑战的市场中保持竞争力。
在下一篇文章中,我们将深入探讨'多时间框架斜率分析:整合短期和长期趋势'这个主题。我们将学习如何在不同时间尺度上应用斜率分析,并如何整合这些信息来做出更明智的交易决策。敬请期待!"







